Minimum Spanning Tree Problems

Bismillahirrahmanirrahim.

Question 1
              
                In the terminology of network theory, what is a tree?  A spanning tree ? A minimum spanning tree?

Ø  Tree – connected undirected graph with no simple circuits

Ø  A spanning tree – Let  Y be a simple graph. A spanning tree of Y is a subgraph of Y that is a tree containing every vertex of Y

Ø  A minimum spanning tree –  spanning tree that has the smallest possible sum of weights of its edges

What is an easy way to recognize a spanning tree?

Ø  All vertices are connected

Ø  No cycle or loops are formed

Ø  Undirected graph

What is the objective of a minimum spanning tree problem?

Ø  To minimise the total cost of the network or to increase the economics efficiency

Ø  To make the transmission of data  to multiple receiving computers more efficient

How many method will solve a minimum spanning tree problrm?

Ø  Kruskal’s Algorithm

Ø  Depth-First Search Algorithm

                        Ø  Prim’s Algorithm

                       What  are  a few types of applications of minimum spanning tree problem?

Ø  Use in the optimization of city natural gas pipeline network

Ø  Application phone network design

Ø  Play a role in data networking such as in  multicasting over Internet Protocol(IP) networks

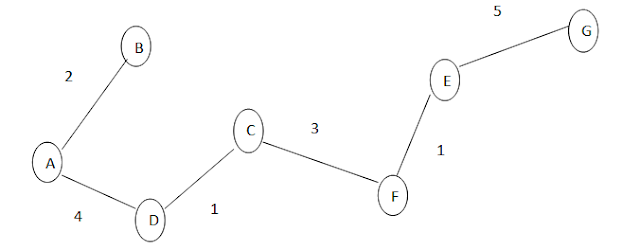
Use a kruskals algorithm to find a minimum spanning tree for a network with the following nodes.

 n = number of vertices;      n-1 = no. of edges of spanning tree

 n = 7

 n -1 = 6

Min. total weight = 1+1+2+4+4+6

                          = 18

Question 2

Case study problems 

The Modern Corp. Problem.

Management of the modern Corp. has decided to have decided to have a state-of-the-art fiber-optic network install to provide high-speed communications (data, voice, and video) between its major centers.

The nodes in figure 1 show the geographical layout of the corporation’s major centers which include corporate headquarters, a supercomputer facility, and a research park, as well as production and distribution centers. The dashed lines are the potential locations of fiber-optic cables. The number next to each dashed line gives the cost (in millions of dollars) if that particular cable is chosen as one to be installed.

Determine which cables should be installed to minimize the total cost of providing high-speed communications between every pair of centers?

number of centers = vertices = n = 7
number of fiber-optic = edges = n - 1 = 7 - 1 = 6

Min. total cost = 1 + 1 + 2 + 3 + 4 + 5
                       = 16 million

Explain the reason for the name minimum spanning-tree.

• the spanning tree with the smallest sum of the distances over the edges in the spanning tree.

Question 3

The Wirehouse Lumber will soon begin logging eight groves of trees in the same general area. Therefore, it must develop a system of dort roads that makes each grove accessible from every other grove. The distance (in miles) between every pair of grove is as follows:

Management now wants to determine which pairs of groves the road should be constructed to connect all groveswith a minimum total length of road.

a) Describe how this problem fits the network description of a minimum spanning tree problem.

because using minimum spanning tree problem it can has the shortest possible sum of distance and connect all the grove. This will easier to the system developer to develop a system of dirt roads that makes each grove accessible from every other grove.

b) Use the suitable algorithm to solve the problem.

number of grove = n = 8
number of roads = n - 1 = 7

= 0.5 + 0.6 + 0.7 + 0.7 + 0.9 + 0.9 + 1.0
= 5.3 miles

Reference
Discrete Mathematics and Its Applications, Sixth Edition, Kenneth H. Rosen

SETS

DEFINITION

Notation: Set usually denoted by capital letter and object/element by lowercase letters.

Example:

            S = { a, b, c , d }

S is a set and  a, b, c , d are called objects/elements that must be in a curly brackets.

Set of number.

 .i)  set of natural numbers , N={ 0,1,2,3,4, … }

.ii) set  of positive integers, P={ 1, 2, 3, 4, … }

iii) set of all integers, Z= { …., -3, -2,-1,0,1,2,3,… }

iv) set of all real numbers, R= { …, -3, -2.5, -1/2, 0, 1, 3/2, … }

APPLICATION OF SETS

You can use sets and set values in other Special Purpose Ledger (FI-SL) subcomponents, such as:

·         Boolean Logic formulas

·         Report Writer

·         Allocations

·         Planning

·         Rollups

·         Currency translation

·         Sets in Boolean Logic Formulas

You use sets in Boolean Logic formulas to refer the system to values that are contained in a set. (The set name is used in a Boolean Logic formula.). You create a basic set called CENTERS that contains cost centers 100, 200, 300, and 400. You then include the set name CENTERS in a Boolean Logic formula:

CCSS-KOSTL IN CENTERS

If you use the Boolean Logic formula as ledger selection criteria, the system checks set CENTERS when selecting data for a ledger. If the data is not for cost center 100, 200, 300, or 400, the data is not selected for posting to the ledger.

Sets in Reporting

The Report Writer uses sets as the building blocks for report rows, columns, cells, and for the data selected for a report. The set hierarchy corresponds to the hierarchy of row and column totals in a report.You can use sets to create simple or complex reports.

Sets in Allocations

You can use sets in allocations to:

·         Select data records from which data should be allocated (sender)

·         Determine to which records data should be allocated (receiver)

·         Define the method of allocation (sender control and receiver control)

You create a basic set called CENTERS that contains specific cost centers. When you use the set as a receiver set, data is allocated to all of the cost centers in the set CENTERS.

Sets in Planning

You use sets in planning to control which objects are used for planning, and the order in which you enter planning data. With sets, you can determine which accounts should be planned within a group of cost centers. A set can also determine the order in which the accounts are planned. For plan variant 01, you can determine that only accounts in the set OHD-ACCT that use cost centers in the set CENTERS can be used for planning. The accounts are planned according to the order they appear in the set OHD-ACCT.

Sets in Rollups

You use sets in rollups to select which data is to be summarized in the rollup ledger. You can also use sets to determine how data should be replaced or reset in a rollup ledger. For example, you use the set OHD-ACCT to select only overhead accounts to be rolled up into a ledger.

Sets in Currency Translation

You can also use sets in defining currency translation methods.You create a set that contains certain transaction types, such as acquisitions and depreciation. You then use the set to limit a currency translation method to only financial statement items that contain the transactions found in the set.

Applications of Logics

Bismillah.

The logic we are considering here is just formal, symbolic or mathematical logic, and our purpose is to separate out the use of logic from study of or research in logic (though research into something other than logic would count).

A majority of people who take an interest in logic prefer to study logic, to advocate the use of logic, or even to build tools to support the use of logic, rather than to actually use logic. It is also not uncommon to find great aspirations, but little substance, even among great philosophers such as Descartes, Leibniz and Hobbes.  

Many different aspects of software engineering, from database management, through programming language design to artificial intelligence have benefitted from the discoveries of modern logic. 

Mathematics, always a deductive science, was the target application for the modern revolution in logic. Its has been transformed by modern logic, and can expect more revolution to come. 

Digital hardware is called "logic", its built up from electronic devices selected to behave like boolean operations, and it is the most pervasive and simple application of logic. 

Many philosophers have sought to emulate the deductive rigour of mathematics, but none have succeeded. Though Russell and the logical positivists hoped modern logic would make this possible, success remains illusory. 

Probably the most successful application has been in the development of relational databases. Logic here plays a role in the theory behind the databases, and may permit certain aspects of the operation of the daTabase to be viewed as analagous to automatic theorem proving. 

Logic is also used in different ways to build logic databases, usually intended to deliver an element of artificial intelligence. 

Logic Programming Similar techniques are applicable more generally, without the emphasis on database management, under the rubrick "logic programming".

The marriage of logic programming with linear programming techniques has enabled rapid and efficient solutions to many difficult scheduling type problems.